The coherence length of a source can be described by L_C=\frac{\lambda}{\Delta \lambda}, where \lambda is the center wavelength of the source and \Delta \lambda is the spectral bandwidth.
Using either manufacturer data or knowing the source specifications we wish to simulate we can estimate the coherence length and build optical systems to observe interference effects.
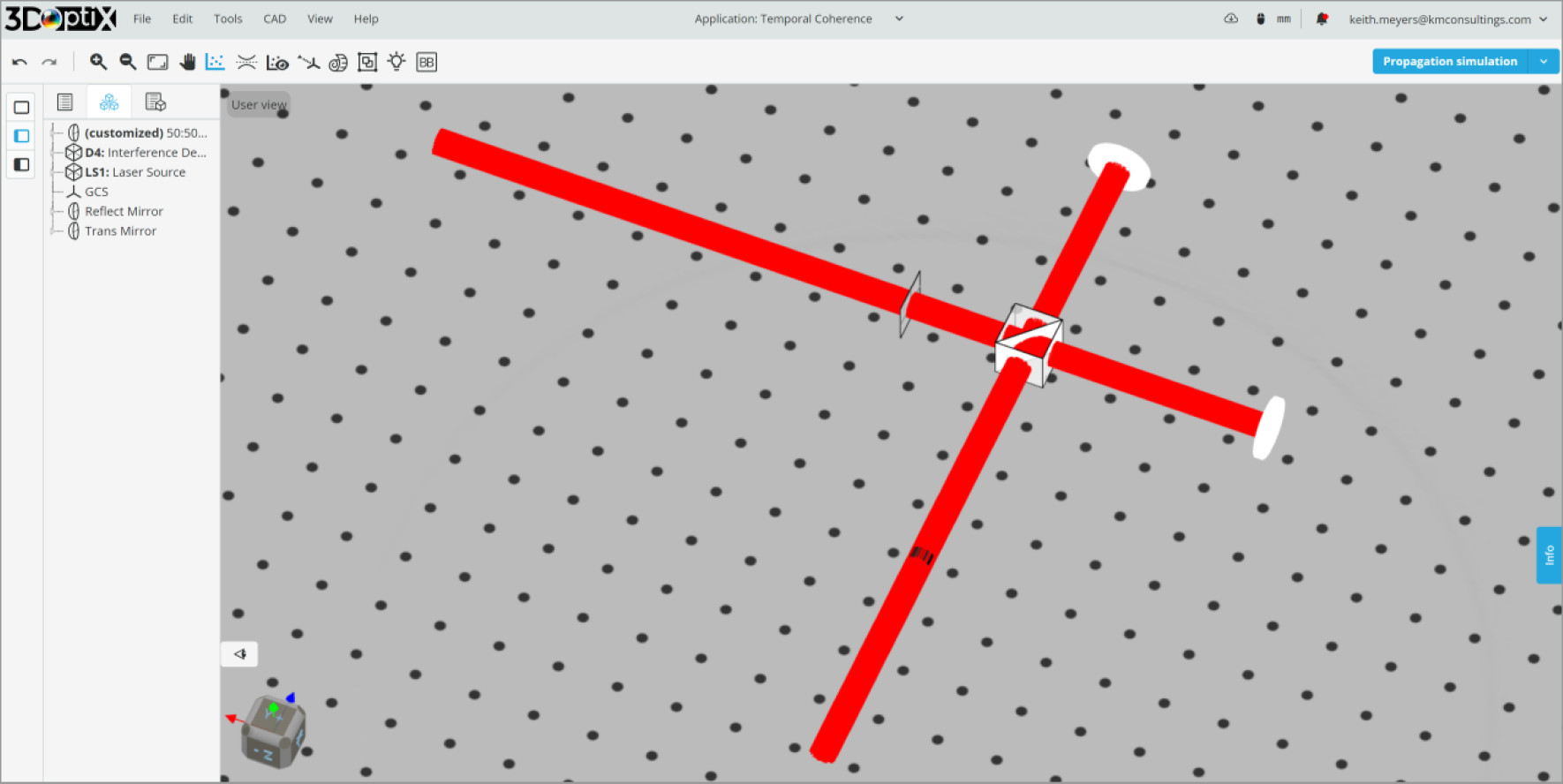
In 3DOptix cloud-based simulation tool these systems can easily be designed and tested using the light sources, optics, and analysis features available. We will overview one application with use cases to get more familiar with these designs.
- Perfect Dielectric 1” Mirror
- Perfect Dielectric 1” Mirror
- Perfect 1” Cube Beamsplitter 50:50 (R:T) Uncoated
- Light Source
- Plane Wave
- Rectangular, 5×5 mm half dimensions
- 633 nm wavelength
- Power, 1 W
- Unpolarized
- Detector: Illumination
- Spot: Coherent Irradiance
- Analysis Rays: 1 million
- 500×500 pixels
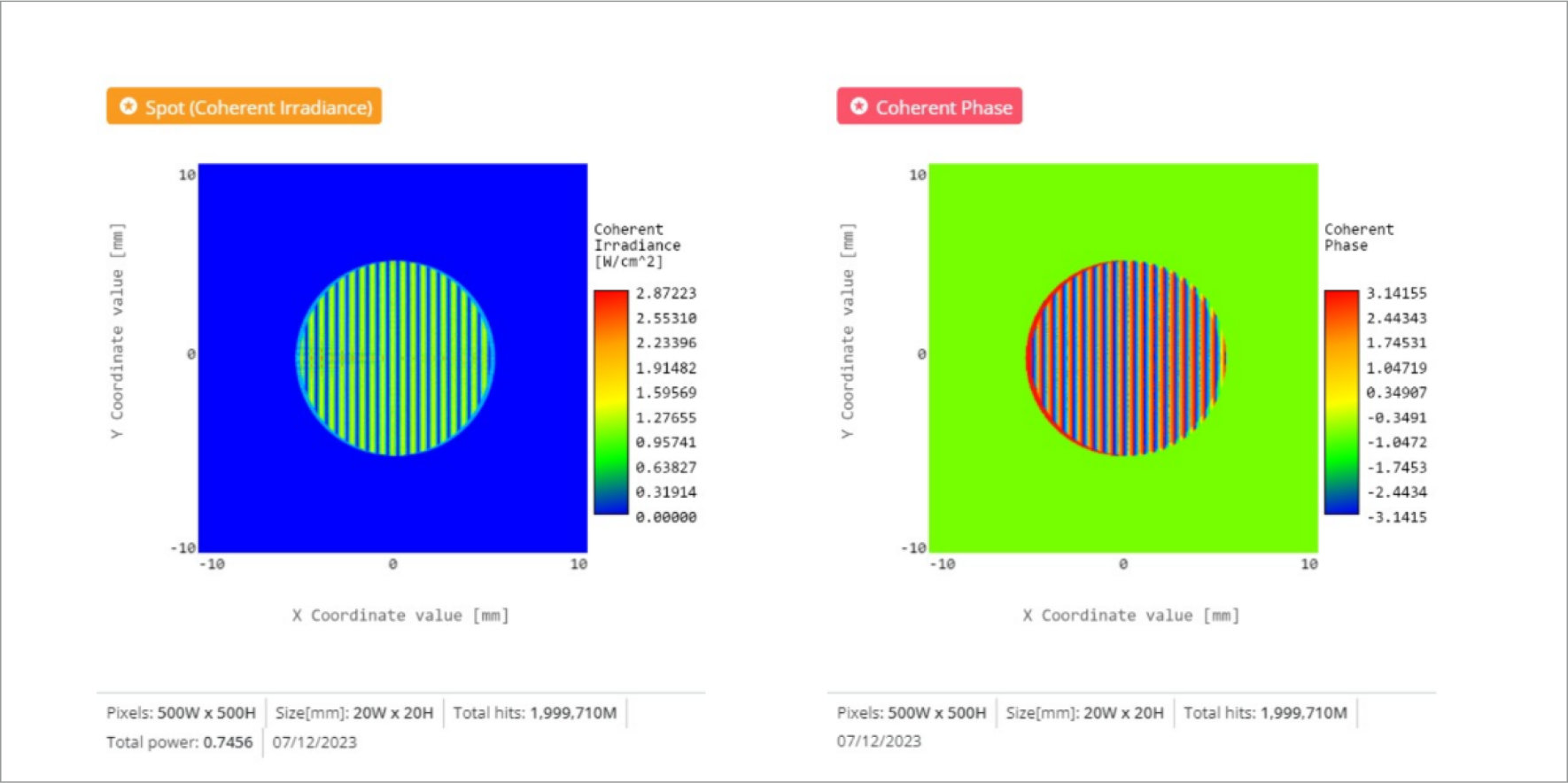
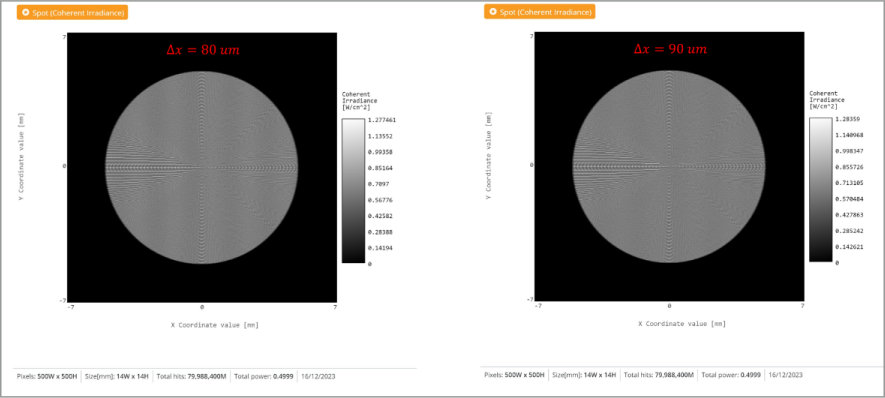
This is the idea behind Fourier Transform Infrared (FTIR) spectrometers that measure the spectrum of a light source. Moving the reference mirror through a certain distance will allow one to measure the spectrum using the interference fringes, and once you have moved the mirror through one full cycle the pattern repeats. By altering the reflected path mirror we can experimentally confirm that the coherence length we calculate is accurate.
An additional parameter we want to use for the plane wave light source is the SPECTRUM TYPE. By including additional wavelengths to simulate an LED we can change the coherence length previously described.
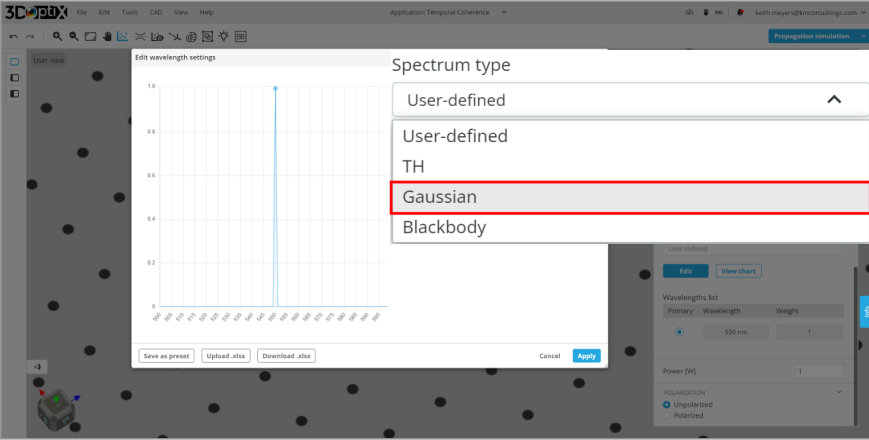
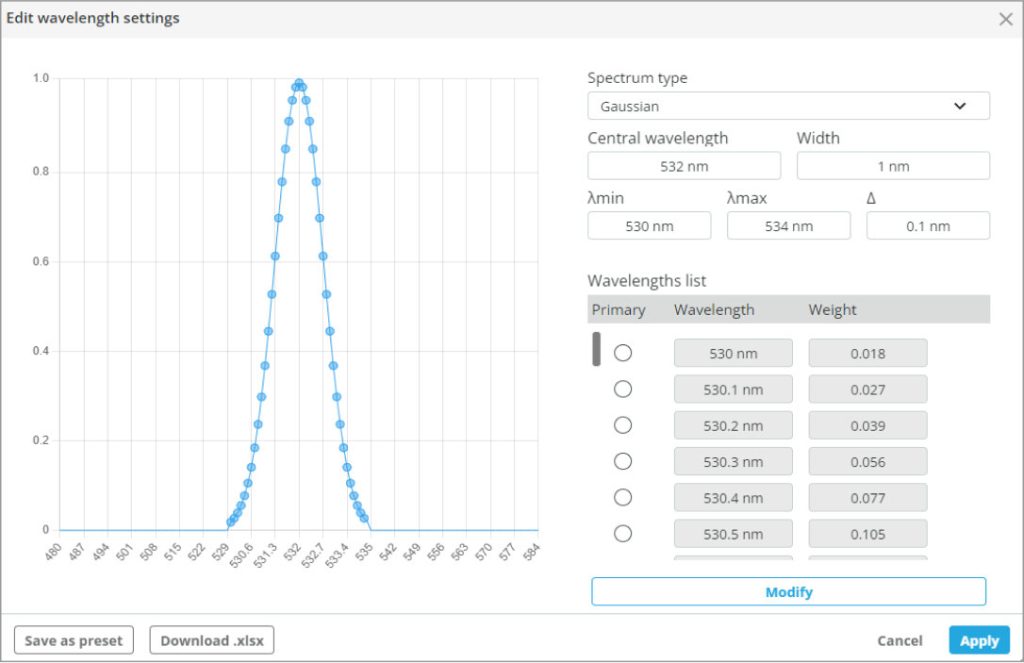
For this system, we will add a GAUSSIAN spectral distribution around the central wavelength of 532 nm. This will change our coherence length from infinite, due to the single wavelength, to some finite length.
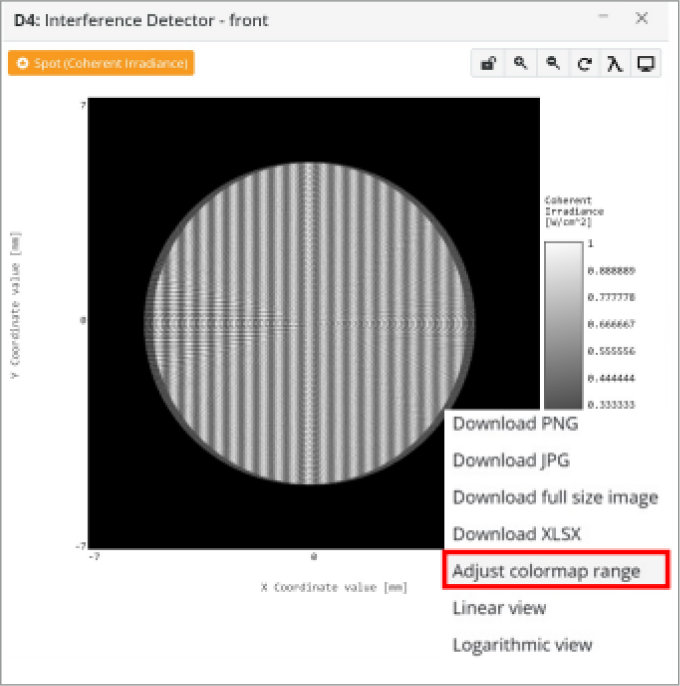
If we click on the analysis image it will pop out into its own window and on the bottom right, we can click on the three bars icon. This will bring up the options drop-down.

We can calculate the coherence length of the simulated light source based on our user generated spectral width of 1.7 nm FWHM.
The coherence length in our simulated light source is thenLC = 166 um. We have achieved observable fringes for a total path length of 160 um, which agrees well with theory.