Diffraction is a phenomenon that occurs when waves encounter obstacles or pass through narrow openings, causing them to bend and spread out. It is a characteristic behavior of all types of waves, including light. When light waves encounter an obstacle or a slit that is comparable in size to the wavelength of light, they diffract and create a pattern of alternating light and dark regions known as a diffraction pattern.
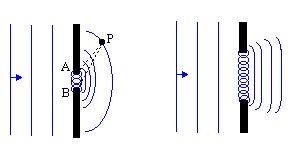
Huygens’ principle, proposed by Dutch physicist Christiaan Huygens, is a fundamental concept used to explain the phenomenon of diffraction. According to Huygens’ principle, every point on a wavefront can be treated as a new source of secondary spherical wavelets. These wavelets combine to form the overall pattern of the diffracted wave. This principle helps us understand how waves propagate and interact with obstacles and openings, leading to the observed diffraction effects.
Huygens’ principle is particularly significant because it provides a way to explain various wave phenomena, including diffraction, in a simple and intuitive manner. By considering each point on a wavefront as a source of secondary wavelets, the principle allows us to understand how the wavefront evolves as it propagates through space.
The Huygens integral, derived from Huygens’ principle, is a mathematical representation used to calculate the diffraction pattern resulting from a given diffracting object. It involves integrating the contributions of the secondary wavelets across the entire diffracting aperture to determine the resulting wavefront. The Huygens integral is a powerful tool in wave optics, enabling the prediction and analysis of diffraction patterns in various situations.
GPU-based implementations of Huygens’ integral can greatly accelerate the simulation of diffraction patterns, enabling researchers to study complex scenarios with higher accuracy and faster turnaround times. This can be particularly beneficial in fields such as optics, where the analysis of intricate diffraction phenomena plays a crucial role in designing optical systems and devices.
The integration of GPU processors in implementing Huygens’ integral offers the potential for significant advancements in simulating and analyzing diffraction phenomena. By leveraging the parallel computing capabilities of GPUs, researchers can explore more complex scenarios, improve accuracy, and accelerate the understanding of wave optics phenomena.
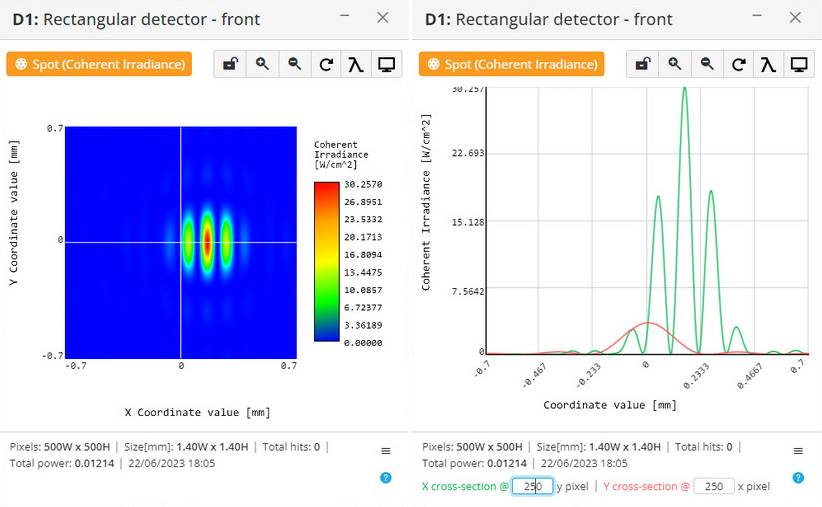
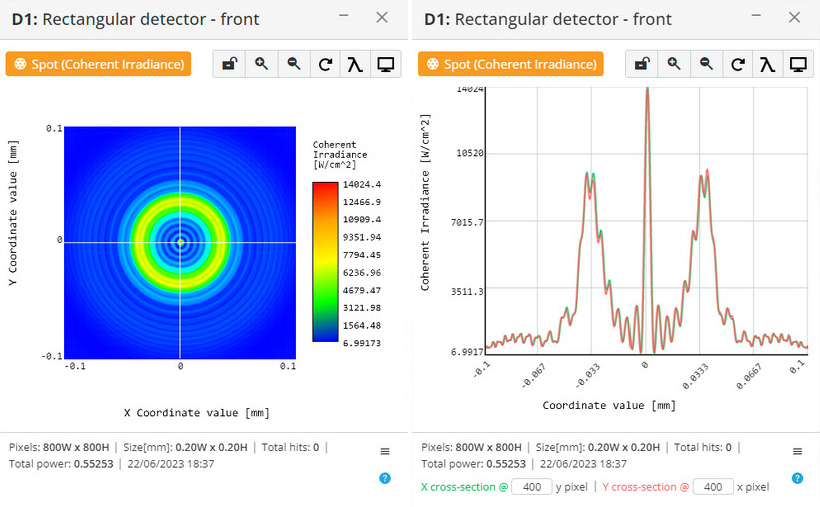
We have implemented a GPU-based numerical solution of a modified scalar Huygens integral (Equation 2, Ref. 1) for the near field without any assumptions. The computation time for the present GPU configuration is 3 seconds for 500X500 sampling in the object plane and 500X500 sampling in the image plane. Amplitude and phase masks can be used as elements of the optical scheme, including spherical-phase masks, amplitude and phase grating masks, and phase holograms (thin film approximation). We are now working on implementing a 4-f model based on spherical phase elements for modeling Fourier optics problems.
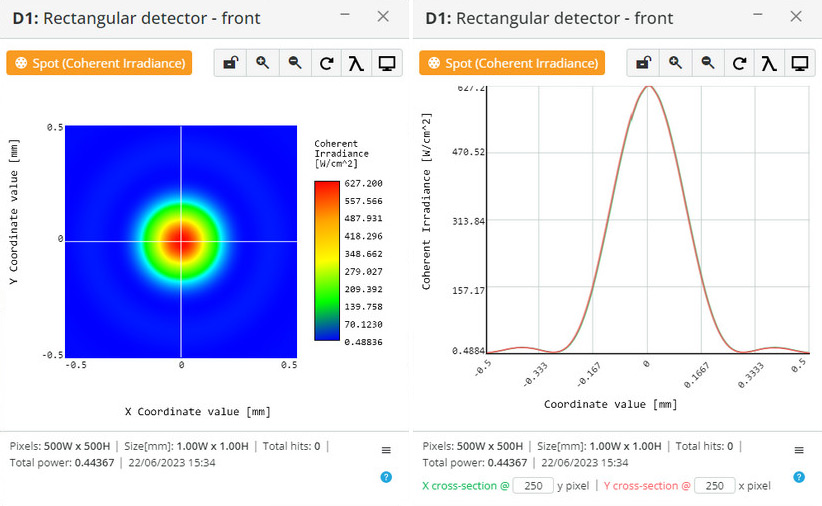
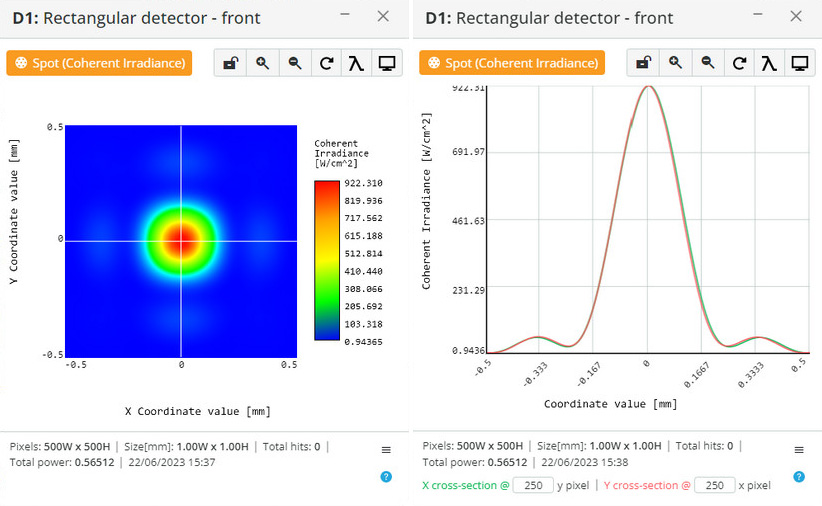
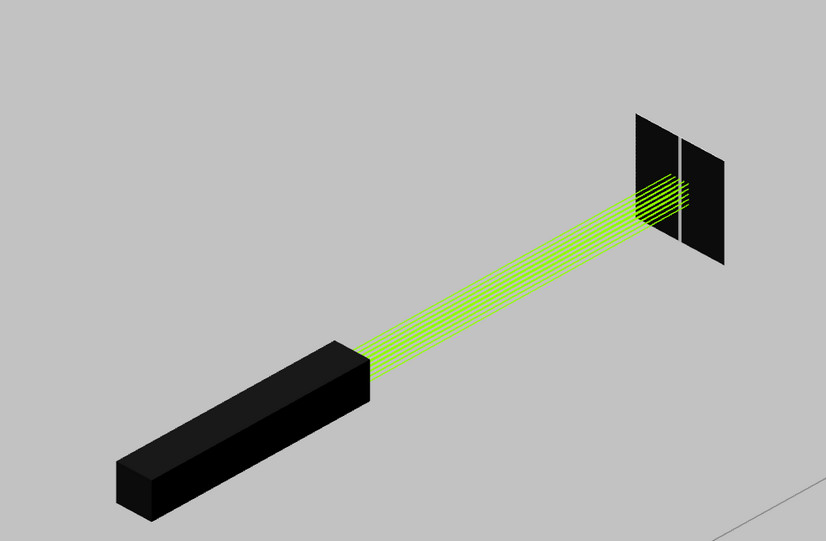
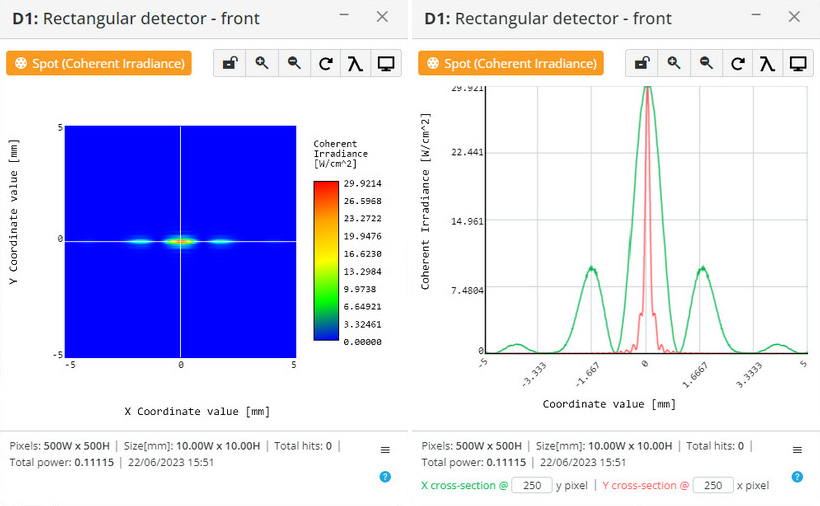
Examples:
Diffraction of circular aperture