One of the fundamental concepts that play a crucial role in optical engineering is that of Gaussian beams. Gaussian beams are special laser beams characterized by their unique intensity distribution and propagation characteristics. Their importance in optical engineering and simulation of optical designs cannot be overstated, as they are a powerful tool in understanding and predicting the behavior of light in various optical systems.
A Gaussian beam is described by its beam waist, which represents the point of minimum beam diameter, and its divergence angle, which determines how the beam expands as it propagates. The intensity profile of a Gaussian beam follows a bell-shaped curve, with the highest intensity at the beam center and decreasing towards the edges. These characteristics make Gaussian beams particularly well-suited for many optical applications. Figure 1 is presented as the 3DOptics calculator of the Gaussian beam. Each beam parameter can be estimated during the definition of other parameters.

Gaussian beams are widely used in optical engineering to model the behavior of light in various optical systems. When light propagates through optical elements such as lenses, mirrors, and waveguides, its interaction can be accurately approximated using Gaussian beam propagation equations. This simplifies the analysis and design process, allowing engineers to predict the beam’s behavior at different points in the system.
In laser systems, Gaussian beams are essential for describing the spatial distribution of the laser light within the resonator cavity. Understanding the properties of Gaussian beams is critical for optimizing the performance of lasers, including maximizing output power, minimizing beam divergence, and achieving a stable and well-defined beam profile.
Gaussian beams can be transformed using optical elements to achieve specific beam profiles and focal characteristics. Beam shaping techniques, such as using diffractive optical elements or spatial light modulators, can modify the intensity distribution of the beam to meet specific application requirements. Additionally, Gaussian beams’ unique focusing properties make them indispensable in applications such as laser cutting, material processing, and medical procedures.
In the simulation of optical designs, Gaussian beam modeling serves as a valuable starting point. Optical design software often employs Gaussian beam approximations to provide initial estimations of the optical system’s performance. These simulations enable engineers to explore different design parameters efficiently and rapidly iterate on potential solutions, saving time and resources in the design process.
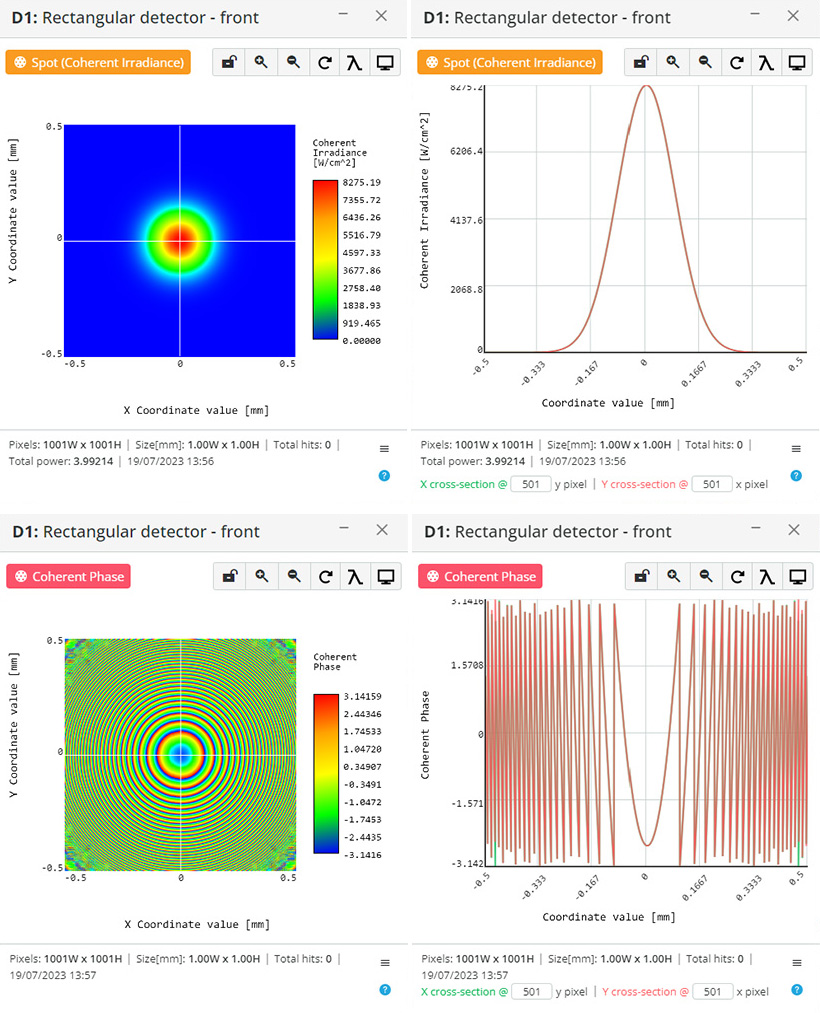
Propagation of the Gaussian beam by Huygens diffraction:
Figure 2 Gaussian beam propagation setup is presented. It consists of a Laser with Gaussian beam waist 0.01 mm, and detector positioned at 10 mm distance from the laser.