Introduction
Rainbows are a meteorological phenomenon, that occurs when light is refracted or bent as it passes through water droplets in the atmosphere. Rainbows, which usually appear as a semi-circular arc of colors, are often seen in the sky after a rain shower or in the vicinity of waterfalls or fountains. They can also be observed when light passes through a prism or a glass of water. Rainbows have long been associated with mythology, folklore, and symbolism and are often seen as a symbol of hope, promise, and renewal. They have inspired many works of art and literature and continue to captivate people’s imaginations to this day.
Yet, the physics of the rainbow is closely related to the interaction of light and matter. In this lesson, the rainbow phenomena will be covered. When sunlight enters a water droplet, it slows down and is bent, or refracted, at an angle. The light is then reflected off the back of the droplet due to total internal reflection. The first order rainbow, which is the most common one, is these rays that are refracted again as it exits the droplet, creating a spectrum of colors, with red on the outer edge and violet on the inner edge. The colors of the rainbow, in order, are red, orange, yellow, green, blue, indigo, and violet (See figure 1). The secondary rainbow is caused by a second total internal reflection that occurs inside the droplet. The second rainbow’s colors are reversed, where red is the interior color and ultraviolet is the exterior color (See figure 1).

The physics of rainbow
The physics of rainbows can be explained by the principles of optics and light refraction. When sunlight enters a water droplet in the atmosphere, it slows down and is refracted, or bent, at a specific angle. The angle of refraction depends on the wavelength of the light, with shorter wavelengths being refracted more than longer wavelengths.
As the refracted light exits the water droplet, it is further refracted again and dispersed into its constituent colors due to the phenomenon of dispersion. This results in a spectrum of colors ranging from red to violet, with red being refracted the least and violet being refracted the most.
The shape of a rainbow is determined by the position of the observer relative to the sun and the water droplets. Rainbows always appear opposite the sun, with the center of the circle of the rainbow appearing at the antisolar point, which is the point directly opposite the sun in the sky. The lower portion of the circle is usually hidden by the ground or horizon, while the upper portion appears as a semicircle in the sky.
In this course, we will focus on finding the angle of the different colors of the rainbow and identifying the different orders of rainbows according to the number of reflections inside each droplet. As light travel in any material, it refracts according to Snell’s law. We can calculate the angle at which light will exit as a function of the impact parameter b as shown in Fig. 2.
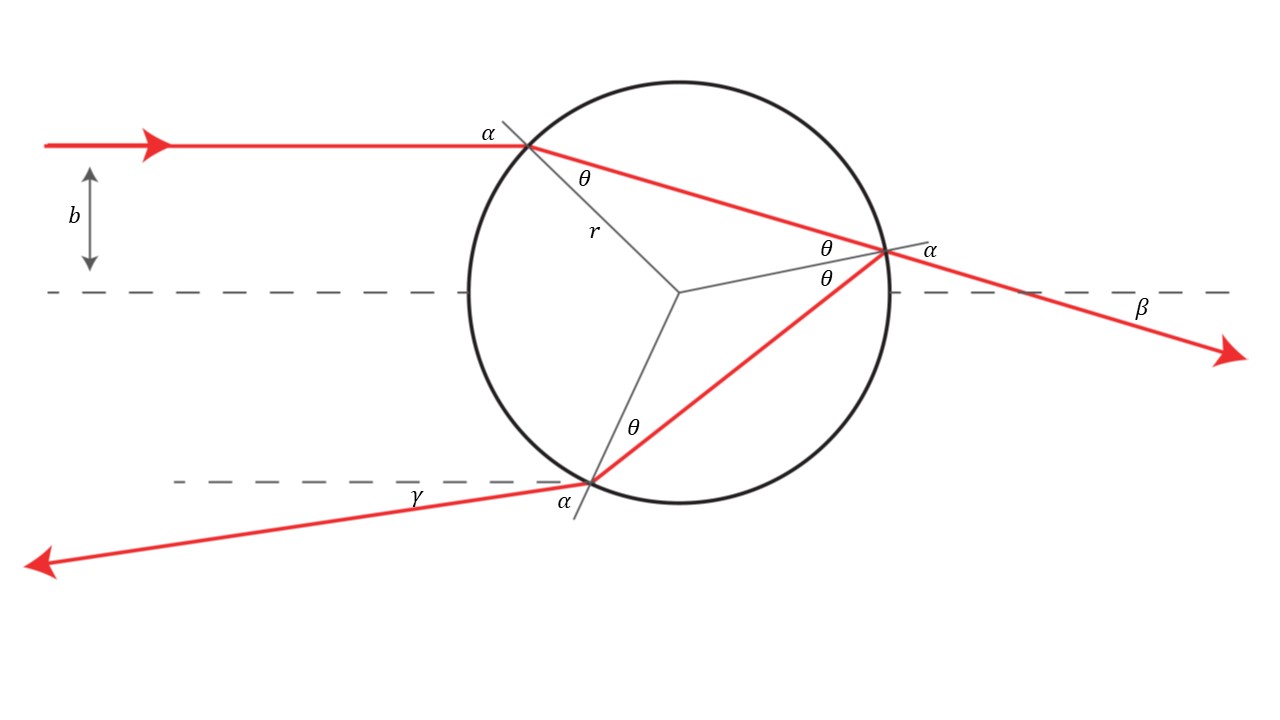
The impact parameter b denotes the distance between the beam of light and the center line of the raindrop. The incident angle is obtained accordingly:
\sin\alpha\;=\;b/r\\
Where r is the raindrop radius. By Snell’s law, we obtain theta as:
\sin\;\theta\;=\;\frac{\sin\;\alpha}n=\frac b{r\;n}\\
Where n is the index of refraction of the raindrop. Thus, the output angle beta is:
\beta\;=\;2\alpha\;-\;2\theta\\
Which is a function of the index of refraction of the water. Since the index of refraction is a function of the wavelength, each wavelength has a different diffraction angle. However, the light hits many raindrops with different impact parameters, so all these colors are mixed and we see white light. There is no rainbow from the refraction through the raindrop.
Exercise 1:
- Load the file “Rainbow_ex.opt” (press the button below to download the file) and run the simulation. And look at the refraction and reflection by the two detectors.
- Measure the angle of the refracted light and the first reflection as a function of the impact parameter for three different wavelengths: 400 nm (blue light), 500 nm (green light), and 600 nm (red light). Fill in the following table
| Wavelength [nm] | Impact parameter [mm] | Output angle beta | Output gamma |
| 400 - blue | 5 | ||
| 400 - blue | 10 | ||
| 400 - blue | 15 | ||
| 400 - blue | 20 | ||
| 500 - green | 5 | ||
| 500 - green | 10 | ||
| 500 - green | 15 | ||
| 500 - green | 20 | ||
| 600 - red | 5 | ||
| 600 - red | 10 | ||
| 600 - red | 15 | ||
| 600 - red | 20 |
As seen, all wavelengths have different output beta angles, but since the light is hitting many raindrops in different impact parameters, all these wavelengths are mixing and the result is white light and no rainbow.
However, when we measure the output angle gamma, we see that the angle is not a linear function of the impact parameter but a parabolic function. Thus, there is a maximum angle where we obtain the same output angle for several input impact parameters. This angle is called a stationary angle and is a function of the wavelength and generates the rainbow we see.
We can calculate the output angle as a function of the impact parameter and index of refraction by:
\gamma\;=\;4\beta\;-\;2\alpha\\
Exercise 2:
Measure the stationary angle as a function of the input wavelength and fill the following table:
Next, we can increase the number of reflections in the raindrop and consider the next order. Enter the “optical setting” of the raindrop, by right-clicking the raindrop. Then enter the back and front surfaces and in both, increase the reflection to 2. Please note that now there are also reflections from entering the raindrop, but these reflections are not a function of the wavelength.
| Wavelength [nm] | Stationary angle | Index of refraction |
| 400 | ||
| 500 | ||
| 600 | ||
| 700 |
Exercise 3:
The second reflection leads to a secondary rainbow with a stationary angle which is also a function of the wavelength. Calculate the output angle as a function of the index of refraction and impact parameter and fill in the following table:
| Wavelength [nm] | Stationary angle for secondary rainbow | Index of refraction |
| 400 | ||
| 500 | ||
| 600 | ||
| 700 |
Note that this rainbow has a reverse order of colors since the angle’s dependency and a wavelength function is opposite compared to the first rainbow. We can continue to calculate higher and higher orders of the rainbow, but their intensity is dropping fast. Usually, we will not see more than two rainbows.

